FC01 – Cap 07 – Ex. 14

Enunciado

(FUVEST) Dois automóveis A e B deslocam-se em um longo trecho retilíneo de uma autoestrada, em sentidos opostos. No gráfico estão representadas as velocidades escalares, em função do tempo, dos dois automóveis.

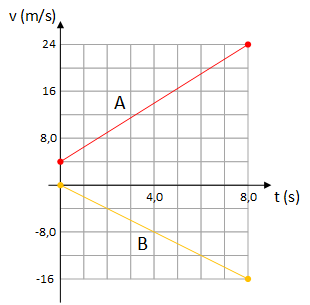
As acelerações escalares dos automóveis A e B, no instante t = 4,0 s, medidas em m/s^2 , são, respectivamente:

1. 3,5 e –2,0
2. 2,5 e 2,0
3. 2,5 e –2,0
4. 3,5 e –3,0
5. 2,5 e –1,5

Entendimento

É uma questão bastante simples que se resolve a partir do gráfico.

Do anunciado temos que os os carros se movem de maneira retilínea, em sentido opostos. O gráfico mostra a variação das velocidades em função do tempo; como as velocidades são representadas por função de primeiro grau, temos que as acelerações são constantes e os automóveis se movimentam em MUV.

Portanto, como as acelerações são as mesmas em qualquer instante no intervalo de 0,0s a 8,0s , especificar de qual instante se pede a aceleração é redundante.

Resolução

O problema pede que se calcule as acelerações para os automóveis A e B no instante t = 4s [\katex]. Como se trata de um MUV, as acelerações são constantes e podemos calcular a aceleração a partir de qualquer intervalo de tempo. Vamos escolher o intervalo mais conveniente, para não evitarmos erros de conta de bobeira e erros de paralaxe.

Assim, para o automóvel A, temos:

a_A = \frac{\Delta v_A}{\Delta t} = \frac{(24 - 4)}{(8 - 0)} = \frac{20}{8} \Rightarrow a_A = 2,5 \enspace m/s^2

Para o automóvel B, temos:

a_B = \frac{\Delta v_B}{\Delta t} = \frac{(-16 - 0)}{(8 - 0)} = \frac{-16}{8} \Rightarrow a_B = -2,0 \enspace m/s^2

A resposta é alternativa C.