FC01 – Cap 08 – Ex. 27

Enunciado

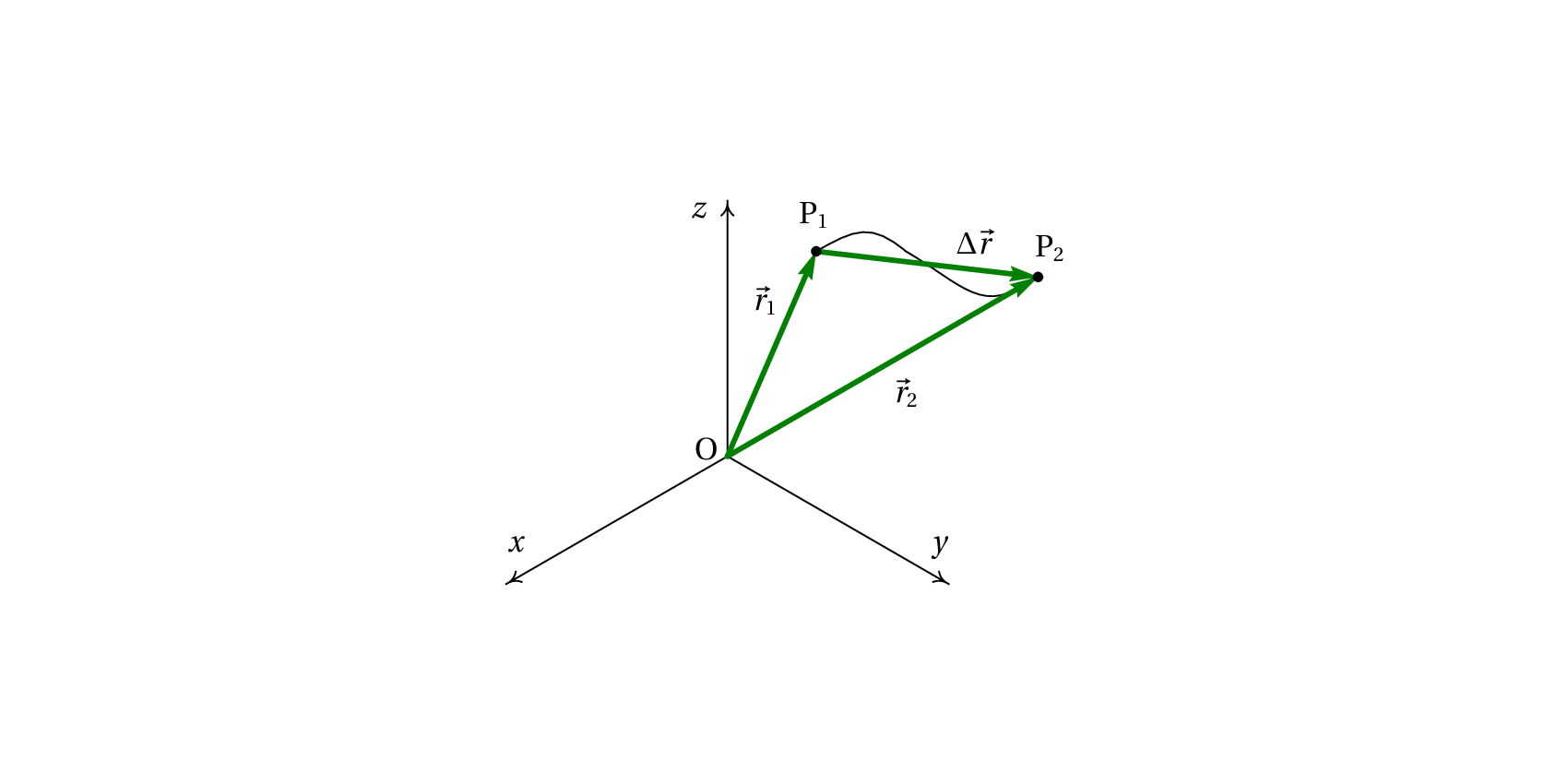
Considere os vetores \vec{w} e \vec{k} representados na figura, com \lvert \vec{w} \rvert = 8 e \lvert \vec{k} \rvert = 6. Determine o vetor \vec{x} tal que \vec{x} = \vec{k} - \vec{w} .

Entendimento

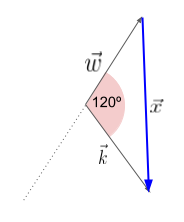
A figura apresentada na questão tem que ser encarada com cautela, pois só podemos iniciar o cálculo depois de algumas transformações.

Essa questão é um pouco sutil pois ela combina dois conceitos: a necessidade de termos vetores “encadeados” para podermos fazer sua adição; e o fato de que a subtração de dois vetores ser a soma do primeiro com o oposto do segundo.

Resolução

Para podermos efetuar a subtração, os vetores têm que estar aplicados num mesmo ponto. Como estão na figura original, a regra não vai funcionar. Assim, temos que “puxar” o vetor \vec{w} ao longo de sua reta de sustentação até que ambos os vetores partam de um mesmo ponto. A subtração de \vec{w} do vetor \vec{k} será o vetor \vec{x} , que parte da “ponta” de \vec{w} e vai até a “ponta” de \vec{k} .

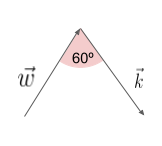
Obtemos assim a figura:

Assim, para calcular o módulo de \vec{x} , usamos a Lei dos Cossenos:

x^2 = w^2 + k^2 - 2wk \cdot cos 120º \\
x^2 = 8^2 + 6^2  - 2 \cdot 8 \cdot 6 \cdot (- \frac{1}{2}) \\
x^2 = 64 + 36 + 48 = 148 \\
x = \sqrt{148} = 2\sqrt{37}