FC01 – Cap 04 – Ex. 38

Enunciado

Um caminhão de comprimento L_1 desloca-se em movimento retilíneo e uniforme (MRU) com velocidade escalar v , estando prestes a ser ultrapassado por um automóvel de comprimento L_2 , também em MRU, com velocidade 3v , no mesmo sentido do caminhão. Sabendo que L_1 = 2 \cdot L_2 , determine o tempo decorrido na ultrapassagem. Dê sua resposta em função de v e L_1 .

Entendimento

Trata-se de um problema clássico de cinemática: dois veículos estão andando em velocidades uniformes, na mesma direção e sentido, sendo que o veículo que vem atrás vem mais rapidamente e terminará por ultrapassar o veículo da frente.

O ponto de atenção em problemas desse tipo é que os veículos não são pontuais e, para ultrapassar totalmente o caminhão, o carro tem que alcançar o caminhão e ainda percorrer a soma dos comprimentos do caminhão e do carro. Isso fica mais claro na figura a seguir:

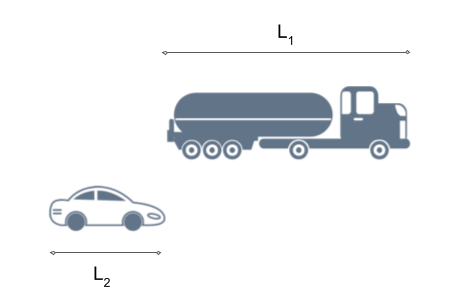
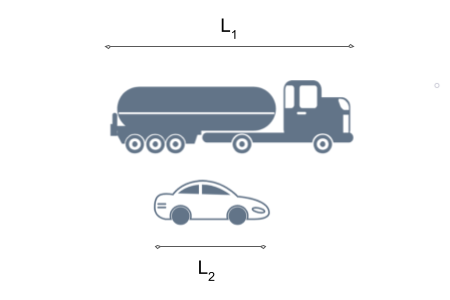
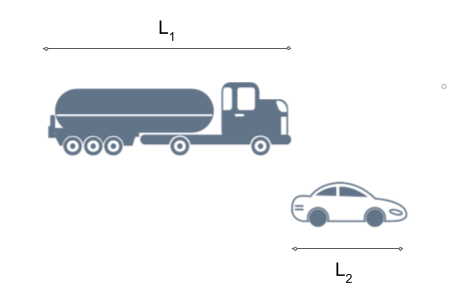
O problema dá as velocidades e comprimentos do caminhão e do carro. Temos apenas que calcular a velocidade do carro em relação ao caminhão e ver a distância que o carro deve percorrer para ultrapassar totalmente o caminhão.

Resolução

O carro tem comprimento L_2 e o caminhão tem comprimento s = L_1 = 2 \cdot L_2 . Para o carro ultrapassar totalmente o caminhão, ele tem que percorrer a distância: s .

s = L_1 + L_2 = L_1 + \dfrac{L_1}{2}

A velocidade do carro em relação ao caminhão é:

v_{2_r} = 3v - v = 2v

Assim, usando a fórmula da equação horária do MU, temos:

s = s_0 + vt \\
\frac{3L_1}{2} =v_{2_r}t \Rightarrow \frac{3L_1}{2} =2vt \\
t = \frac{3L_1}{4v}