FC01 – Cap 03 – Ex. 73

(UFRGS) Um projétil, com velocidade escalar constante de 300 \enspace m/s , é disparado em direção ao centro de um navio que se move a uma velocidade escalar constante de 10 \enspace m/s em direção perpendicular à trajetória do projétil. Se o impacto ocorrer a 20 m do centro do navio, a que distância deste foi feito o disparo?

Entendimento

Um problema interessante, em que um míssil é disparado em direção a um navio que se encontra em movimento. O enunciado dá as velocidades do navio e do míssil, tanto um quanto o outro estão em MU.

Do ponto de vista físico, é importante observar que, desde o instante do disparo do míssil até o impacto, o navio percorre uma certa distância, distância dada pelo problema.

Toda a questão pode ser sumarizada nas figuras a seguir:

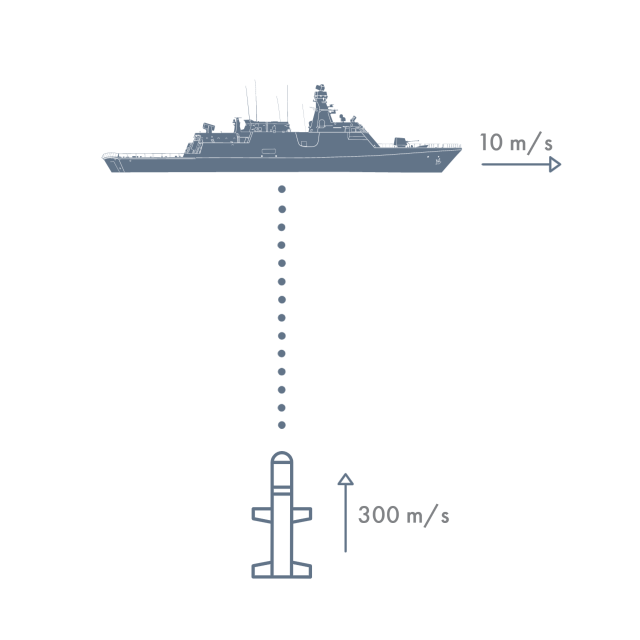
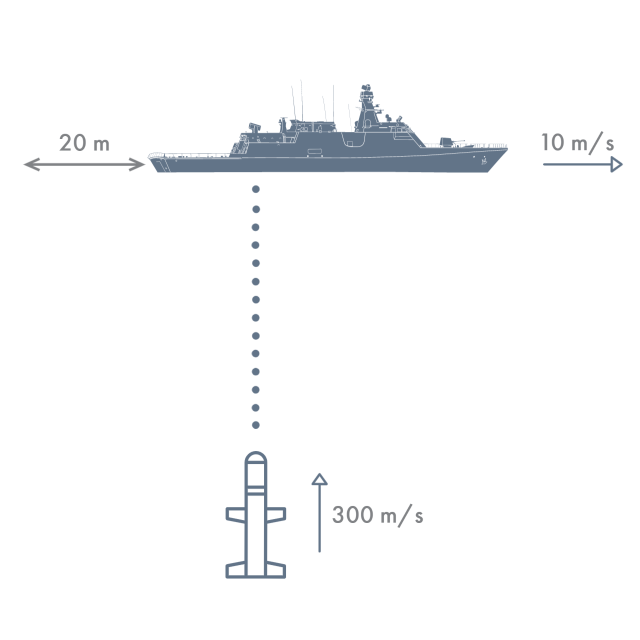
O que a questão solicita é a distância do navio até onde se encontrava o míssil, no instante do disparo.

Bom, se temos a velocidade do navio e a distância percorrida por ele até o impacto, temos o tempo até o impacto. Com este tempo e a velocidade do míssil, poderemos calcular a distância do míssil até o navio.

Resolução

Sabemos que o navio percorreu 20 m [/katex}, então temos:

s_n = s_{0_n} + v_nt \\
20 = 0 + 10t \Rightarrow t = 2 s

Sabendo que o tempo até o impacto, podemos calcular a distância do míssil no momento do disparo:

s_m = s_{0_m} + v_mt \\
s_m = 0 + 300 \cdot 2 \Rightarrow s_m = 600 m

Importante notar que foram usados dois referenciais separados, um para o movimento do navio e outro para o movimento do míssil.