FC01 – Cap 04 – Ex. 53

Enunciado

No Pão de Açúcar, Rio de Janeiro, temos o famoso bondinho suspenso que leva os turistas para o pico do morro. Dois cabos de aço paralelos correm em sentidos contrários, com uma mesma velocidade de módulo 36 \enspace km/h . A foto mostra os bondinhos quando vão se cruzar no meio do caminho.

Tendo cada bondinho uma largura de 6,0 m e um comprimento de 8,0 m , pergunta-se:

1. Por quanto tempo um passageiro que está na janela de um dos bondinhos vê o outro à sua frente, durante o cruzamento?
2. Um turista, no pico do Pão de Açúcar, assiste ao cruzamento dos dois bondinhos. Quanto tempo dura o cruzamento?

Entendimento

O problema apresenta o cruzamento dos bondinhos do Corcovado, com MU. O problema dá ainda as dimensões do bondinho (por sinal, a largura é uma informação desnecessária).

É um problema de velocidade relativa no qual temos que ficar atentos quanto ao referencial, caso contrário, a solução não sai.

Resolução: item a.

Para um passageiro de um dos bondinhos, a velocidade relativa do outro bondinho é de 36 km/h + 36 km/h = 72 km/h . Mas 72 km/h = 72 \cdot 1.000 / 3.600s = 20 m/s

Um passageiro só vai ver o outro bondinho, enquanto um bonde estiver na frente do passageiro. Assim, o passageiro vê o bondinho enquanto os 8 m de seu comprimento passam na frente do passageiro, como na figura a seguir:

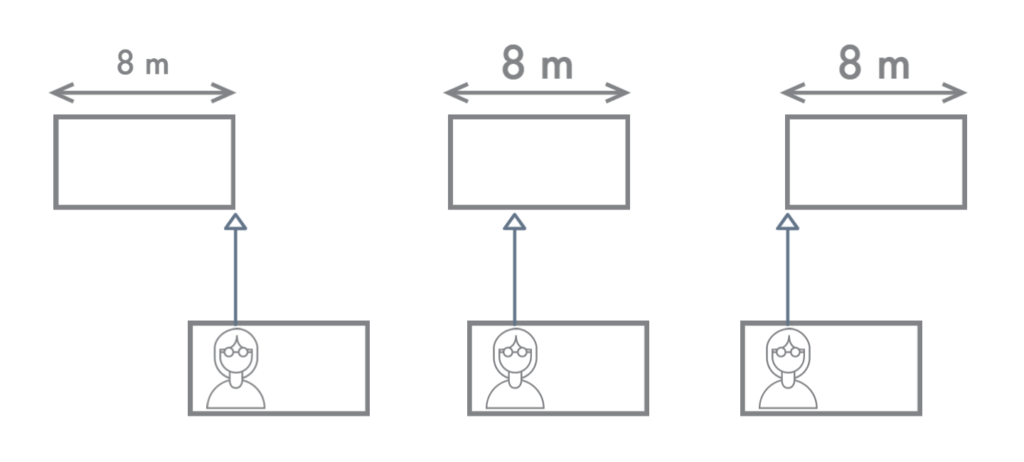
Portanto,

\begin{align*}
& 20m -\!\!\!-\!\!\!- 1 s \\
& 8m \enspace -\!\!\!-\!\!\!- t_1 \\
\end{align*} \\
\therefore t_1 = 0,4s

Resolução: item b.

Para um observador no solo, um bondinho cruza completamente o outro quando ele ultrapassa dois comprimentos de de bondinho, como esquematizado na figura a seguir:

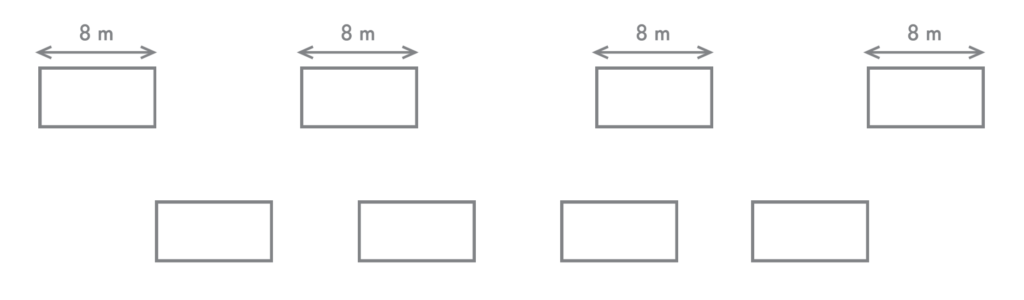
Como a velocidade relativa entre os bondinhos permanece a mesma, mas a distância percorrida dobra, comparação ao item anterior, o cruzamento levará o dobro do tempo do item a. Portanto, T_2 = 0,8 s .