Address
304 North Cardinal St.
Dorchester Center, MA 02124
Work Hours
Monday to Friday: 7AM - 7PM
Weekend: 10AM - 5PM
Address
304 North Cardinal St.
Dorchester Center, MA 02124
Work Hours
Monday to Friday: 7AM - 7PM
Weekend: 10AM - 5PM
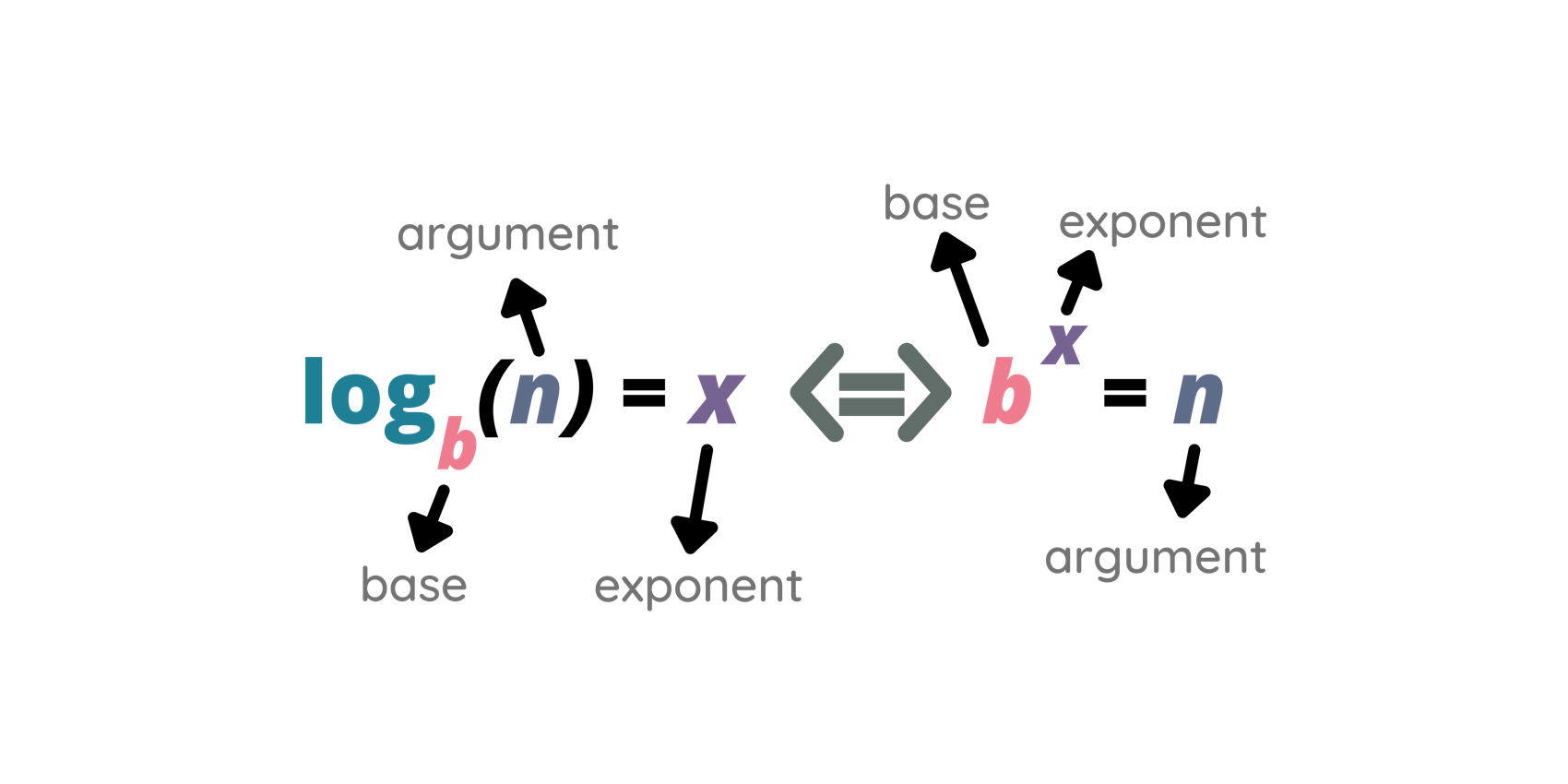
Se \log_{ab} a = 4 , calcule \log_{ab} \dfrac{\sqrt[3]{a}}{\sqrt{b}} .
Questão de aplicação de propriedades de logaritmos, mas temperada por uma necessidade de mais iniciativa por parte do aluno. Não é uma questão complexa, mas um pouco capciosa, no sentido de exigir essa dose extra de iniciativa.
Vamos resolver a questão em duas etapas, a primeira dedicada a trabalhar a primeira expressão dada pela questão:
\log_{ab} a = 4 \Rightarrow a = (ab)^4 \Rightarrow a = a^4 \cdot b^4 \Rightarrow b = \sqrt[4]{\dfrac{1}{a^3}} \\
\enspace \\
\therefore b = a^{\frac{-3}{4}}Trabalhando a segunda expressão, temos:
\log_{ab} \dfrac{\sqrt[3]{a}}{\sqrt{b}} = \log_{ab} {\sqrt[3]{a}} - {\log_{ab} {\sqrt{b}}} = \frac{1}{3} \log_{ab} a - \frac{1}{2} \log_{ab} b = \\
\enspace \\
\text{Sabendo que: } \log_{ab} a = 4 \text{ e que: } b = a^{\frac{-3}{4}} \text{, temos:} \\
\enspace \\
= \frac{1}{3} \log_{ab} a - \frac{1}{2} \log_{ab} b = \frac{1}{3} \cdot 4 - \frac{1}{2} \cdot \log_{ab} a^{\frac{-3}{4}} = \\
\enspace \\
= \frac{4}{3} - \frac{1}{2} \cdot \left( \frac{-3}{4} \right) \cdot \log_{ab} a = \frac{4}{3} + \frac{3}{8} \cdot 4 = \frac{4}{3} + \frac{3}{2} = \frac{17}{6}