FME02 – Cap 03 – Ex. 184

Enunciado

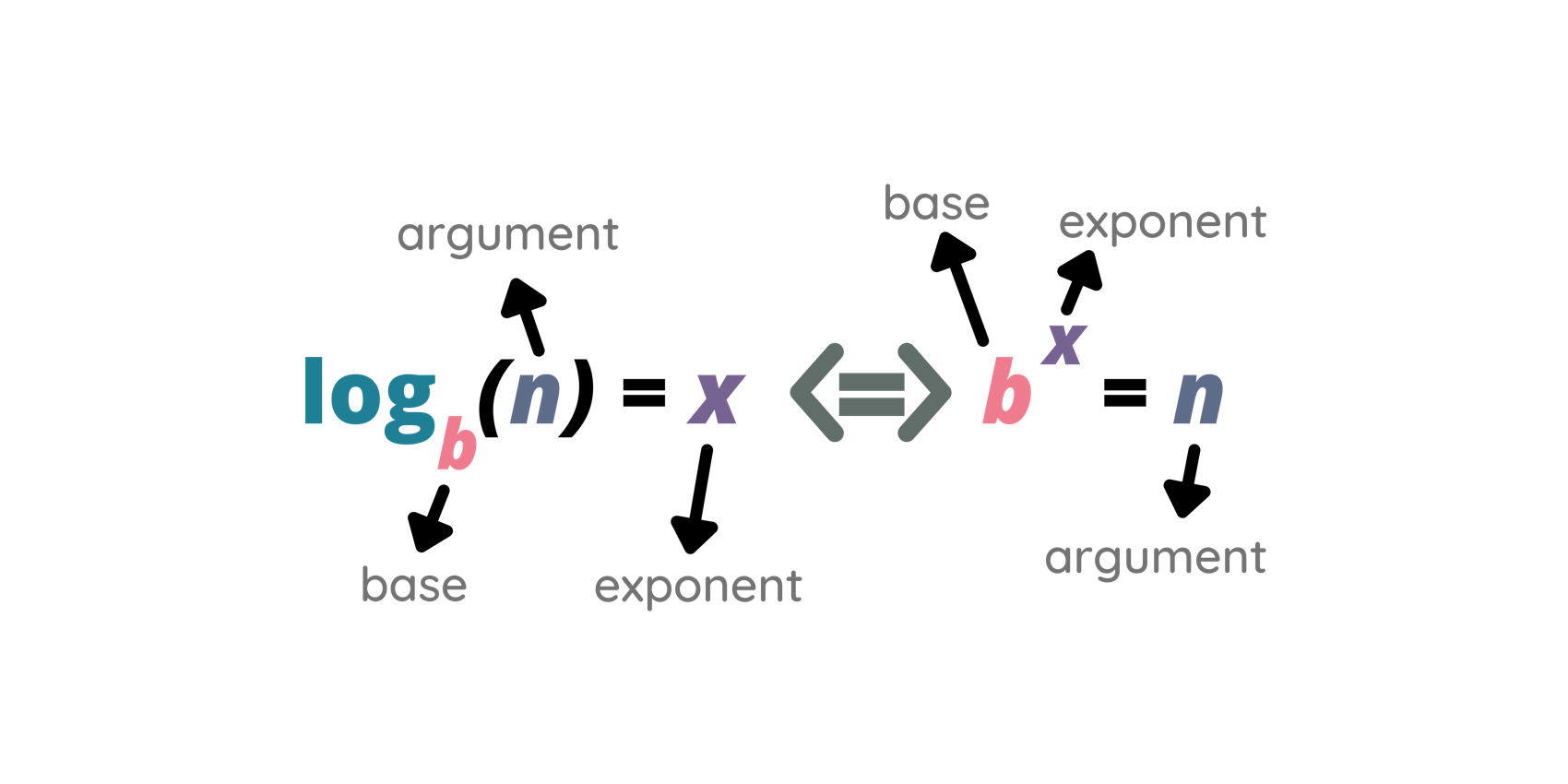
Determine o valor de

\log_3 2 \cdot \log_4 3 \cdot \log_5 4 \cdot \log_6 5 \cdot \log_7 6 \cdot \log_8 7 \cdot \log_9 8 \cdot \log_{10} 9

Entendimento

Outra questão de aplicação das propriedades de logaritmos que exige um pouco de maturidade do aluno. A estratégia em questões como essa é sempre buscar uma base conveniente, no caso em particular a busca é por bases convenientes.

Outro aspecto a considerar é que, muitas vezes, em questões que apresentam um produto de vários fatores, quase sempre a solução passa por um corta-corta de fatores no numerador com fatores no denominador.

A maturidade do aluno vem de encarar essas questões com desconfiança, perguntando a si mesmo “e se eu fizer isso?” e fazer alguma experimentação. Como logaritmos têm várias propriedades, a experimentação passa por elas. Nesta questão vamos usar a propriedade de mudança de base.

Resolução

Trabalhando as bases dos logaritmos na expressão original, temos:

\log_3 2 \cdot \log_4 3 \cdot \log_5 4 \cdot \log_6 5 \cdot \log_7 6 \cdot \log_8 7 \cdot \log_9 8 \cdot \log_{10} 9 = \\
\enspace \\
= \frac{\log_{10} 2}{\log_{10} 3}  \cdot \frac{\log_{10} 3}{\log_{10} 4}  \cdot \frac{\log_{10} 4}{\log_{10} 5}  \cdot \frac{\log_{10} 5}{\log_{10} 6}  \cdot \frac{\log_{10} 6}{\log_{10} 7}  \cdot \frac{\log_{10} 7}{\log_{10} 8} \cdot  \frac{\log_{10} 8}{\log_{10} 9} \cdot \log_{10} 9 = \log_{10} 2