FME02 – Cap 03 – Ex. 188

Enunciado

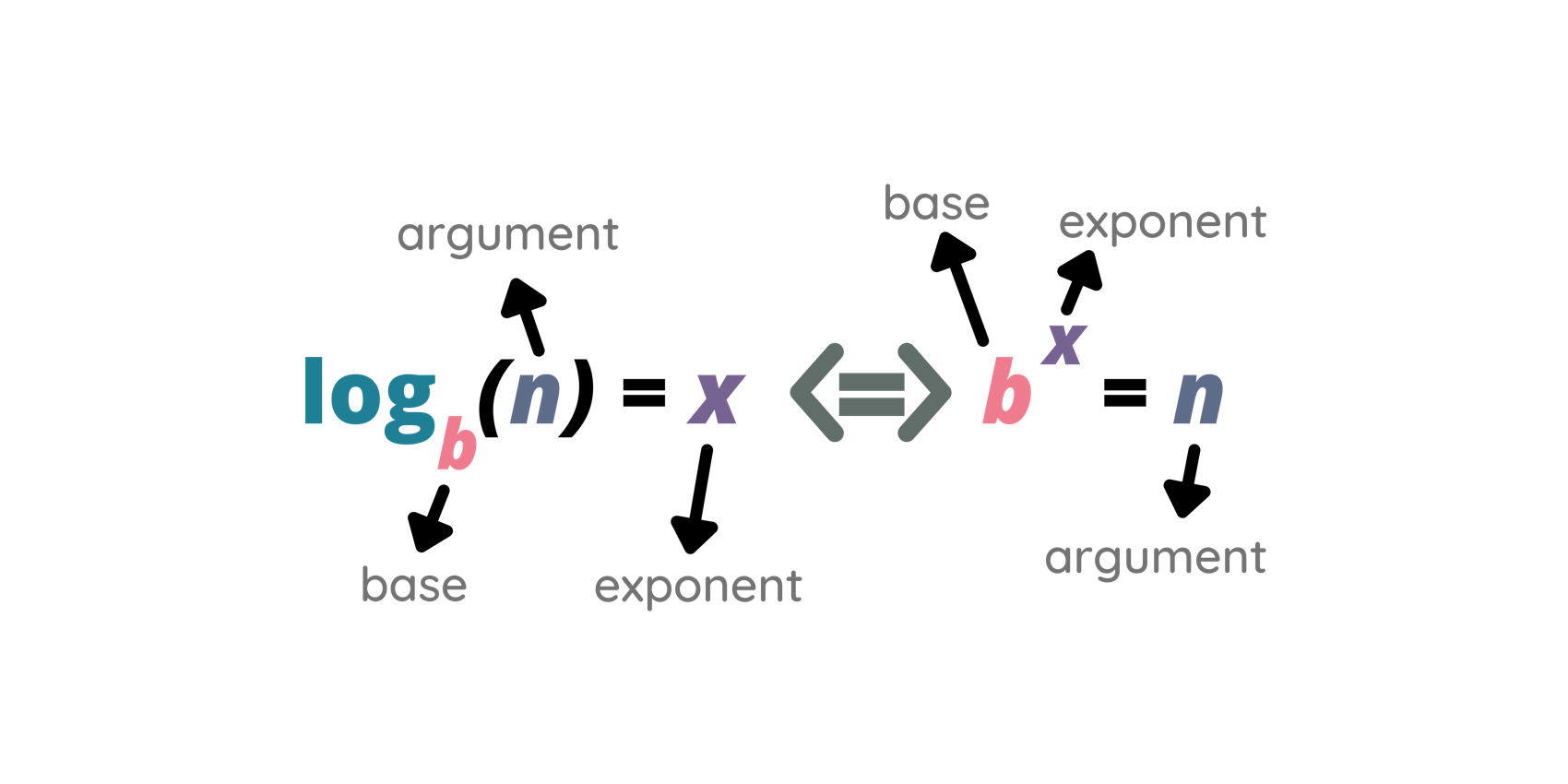
Simplifique a^{\log_a b \cdot \log_b c \cdot \log_c d} .

Entendimento

Este tipo de exercício exige apenas a aplicação da definição de logaritmo e de suas propriedades, mas tende a assustar o aluno com menos iniciativa.

O caminho é pensar em mudança de base, já que queremos simplificar o produto de logaritmos que está no expoente. Quase sempre queremos chegar num corta-corta do produto em que numeradores são cancelados por denominadores e o produto inteiro se simplifica.

Resolução

A partir da expressão original, temos, mudando a base dos logaritmos do expoente:

a^{\log_a b \cdot \log_b c \cdot \log_c d} = \\
\enspace \\
a^{\log_a b \cdot \frac{\log_a c} {\log_a b} \cdot \frac{\log_a d} {\log_a c}} = \\
\enspace \\
a^{\log_a d} = d

Caso não queiramos empregar a propriedade de logaritmos que usamos na última expressão acimas, podemos fazer a^{\log_a d} = x e, pela definição de logaritmo chegamos no mesmo resultado:

a^{\log_a d} = x \Rightarrow \log_a d = \log_a x \Rightarrow x = d