Address
304 North Cardinal St.
Dorchester Center, MA 02124
Work Hours
Monday to Friday: 7AM - 7PM
Weekend: 10AM - 5PM
Enunciado
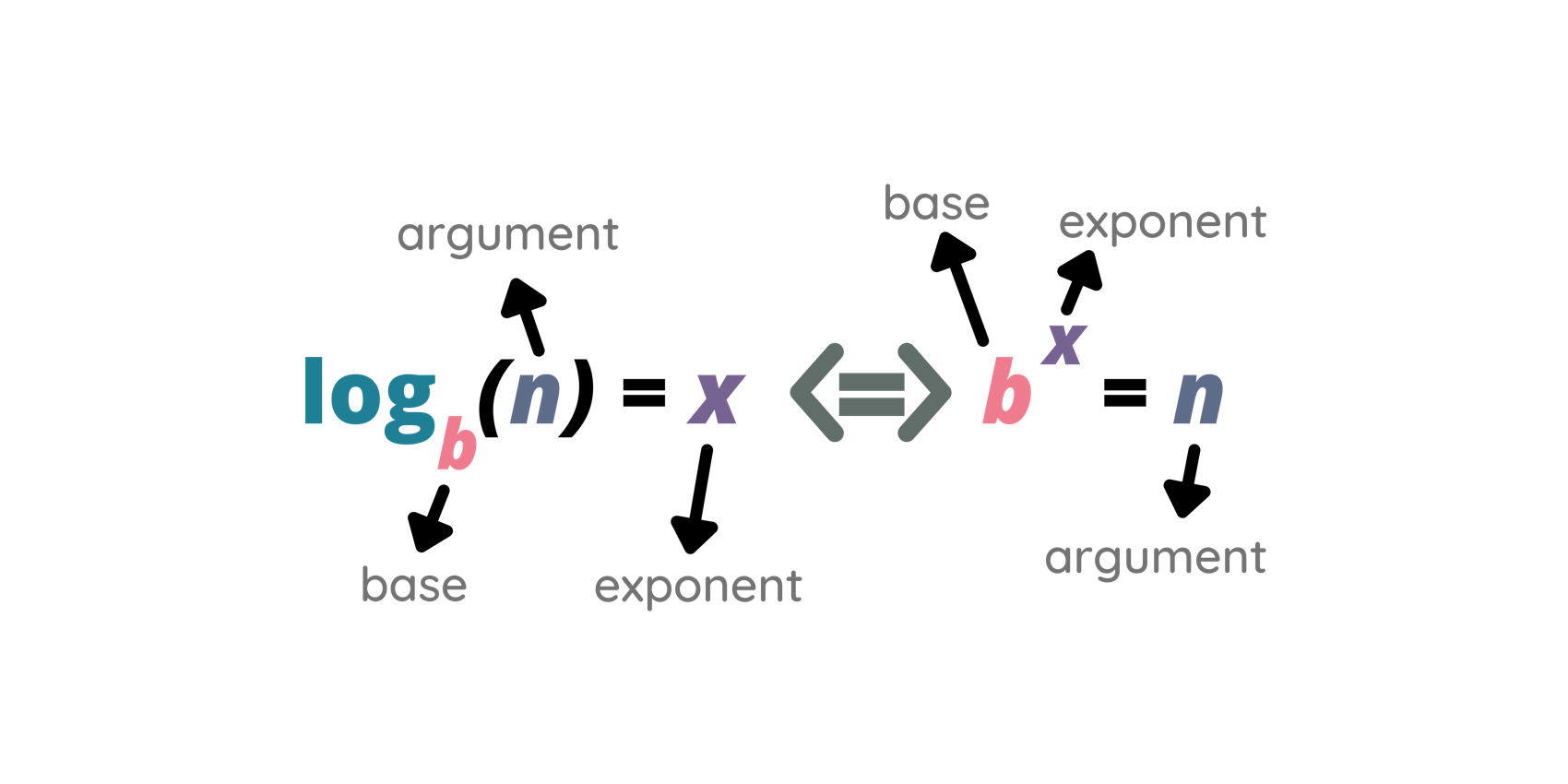
Se a, b, c e d são reais positivos, diferentes de 1 e a \cdot b \ne 1 , prove que:
\log_a d \cdot \log_b d + \log_b d \cdot \log_c d + \log_c d \cdot \log_a d = \frac{\log_a d \cdot \log_b d \cdot \log_c d}{\log_{abc} d}Entendimento
Esta demonstração exige uma boa dose de iniciativa do aluno pois não é apenas uma aplicação direta das propriedades de logaritmos. É preciso buscar algumas transformações intermediárias que não são muito usuais, bem como aplicar as propriedades de logaritmos.
A chave é olhar a expressão que se quer obter, a do lado direito da igualdade, e fazer algumas experimentações. É um exercício que requer um certo esforço do aluno.
Resolução
Olhando a expressão do lado direito da igualdade que se quer demonstrar, observamos que existe um \log_{abc} , assim, uma ideia de solução seria experimentar uma mudança de base generalizada para abc .
Partindo então da expressão do lado esquerdo da igualdade que queremos desmonstrar, temos:
\log_a d \cdot \log_b d + \log_b d \cdot \log_c d + \log_c d \cdot \log_a d = \\
\enspace \\
= \frac{\log_{abc} d}{\log_{abc} a} \cdot \frac{\log_{abc} d}{\log_{abc} b} + \frac{\log_{abc} d}{\log_{abc} b} \cdot \frac{\log_{abc} d}{\log_{abc} c} + \frac{\log_{abc} d}{\log_{abc} c} \cdot \frac{\log_{abc} d}{\log_{abc} a} = \\
\enspace \\
= \frac{(\log_{abc} d)^2}{\log_{abc} a \cdot \log_{abc} b} + \frac{(\log_{abc} d)^2}{\log_{abc} b \cdot \log_{abc} c} + \frac{(\log_{abc} d)^2}{\log_{abc} c \cdot \log_{abc} a} = \\
\enspace \\
= (\log_{abc} d)^2 \cdot \left( \frac{1}{\log_{abc} a \cdot \log_{abc} b} + \frac{1}{\log_{abc} b \cdot \log_{abc} c} + \frac{1}{\log_{abc} c \cdot \log_{abc} a} \right) = \\
\enspace \\
= (\log_{abc} d)^2 \cdot \left( \frac{\log_{abc} c + \log_{abc} a +\log_{abc} b}{\log_{abc} a \cdot \log_{abc} b \cdot \log_{abc} c} \right) = \\
\enspace \\
= (\log_{abc} d)^2 \cdot \left( \frac{\log_{abc} cab}{\log_{abc} a \cdot \log_{abc} b \cdot \log_{abc} c} \right) = \\
\enspace \\
= (\log_{abc} d)^2 \cdot \left( \frac{1}{\log_{abc} a \cdot \log_{abc} b \cdot \log_{abc} c} \right) = \\Podemos multiplicar a última expressão por 1 = \dfrac{\log_{abc} d}{\log_{abc} d} , sem alterar seu valor, assim:
= (\log_{abc} d)^2 \cdot \left( \frac{1}{\log_{abc} a \cdot \log_{abc} b \cdot \log_{abc} c} \right) = \\
\enspace \\
= \frac{\log_{abc} d}{\log_{abc} d} \cdot (\log_{abc} d)^2 \cdot \left( \frac{1}{\log_{abc} a \cdot \log_{abc} b \cdot \log_{abc} c} \right) = \\
\enspace \\
= \frac{1}{\log_{abc} d} \cdot (\log_{abc} d)^3 \cdot \left( \frac{1}{\log_{abc} a \cdot \log_{abc} b \cdot \log_{abc} c} \right) = \\
\enspace \\
= \frac{1}{\log_{abc} d} \cdot \left( \frac{(\log_{abc} d)^3}{\log_{abc} a \cdot \log_{abc} b \cdot \log_{abc} c} \right) = \\
\enspace \\
= \frac{1}{\log_{abc} d} \cdot \left( \frac{\log_{abc} d \cdot \log_{abc} d \cdot \log_{abc} d}{\log_{abc} a \cdot \log_{abc} b \cdot \log_{abc} c} \right) = \\
\enspace \\
= \frac{1}{\log_{abc} d} \cdot \left( \frac{\log_{abc} d}{\log_{abc} a} \cdot \frac{\log_{abc} d}{\log_{abc} b} \cdot \frac{\log_{abc} d}{\log_{abc} c} \right) = \\
\enspace \\
= \frac{1}{\log_{abc} d} \cdot \left( log_a d \cdot \log_b d \cdot \log_c d \right) = \\
\enspace \\
= \frac{log_a d \cdot \log_b d \cdot \log_c d}{\log_{abc} d} \\Dificuldade: 3,75
Entendimento: 2,5
Conceitos: 4,0
Iniciativa: 4,5
Cálculos: 4,0
Conceitos: 4,0
Iniciativa: 4,5
Cálculos: 4,0