Address
304 North Cardinal St.
Dorchester Center, MA 02124
Work Hours
Monday to Friday: 7AM - 7PM
Weekend: 10AM - 5PM
Address
304 North Cardinal St.
Dorchester Center, MA 02124
Work Hours
Monday to Friday: 7AM - 7PM
Weekend: 10AM - 5PM
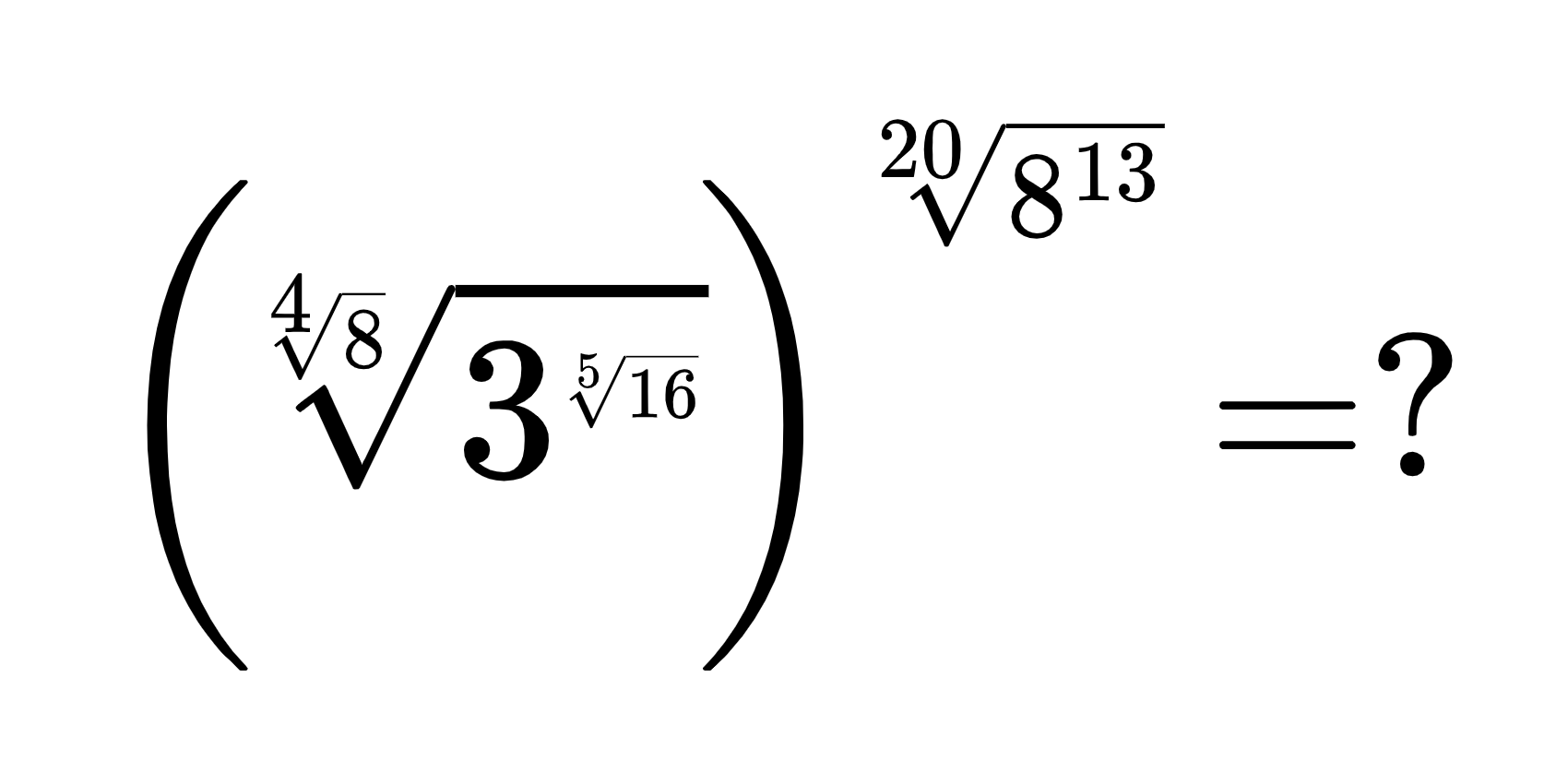
Calcule:
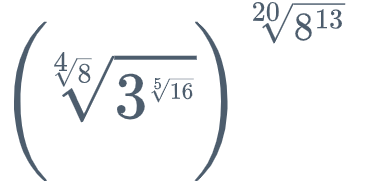
Sou forçado a reconhecer que a expressão, à primeira vista, assusta um pouco.
Este é o típico exercício que exige muita iniciativa do aluno, experimentação mesmo, pois não é claro qual é o caminho a seguir. Além disso, o aluno vai ter uma certa tendência a fugir da expressão, mas se ele observá-la mais detidamente e se lembrar das propriedades da exponenciação, pode encontrar a solução.
É preciso ter muita firmeza com a notação matemática também, pois é arriscado cometermos erros nas contas em expressões complexas como essa.
O caminho que iremos seguir é transformar todas as raízes em expoentes, usando as propriedades:
\sqrt [n] {a^m} = a^{\frac{m}{n}} \\
\enspace \\
a^m \cdot a^n = a^{m+n} \\
\enspace \\
(a^m)^n = a^{m \cdot n}Para melhor visualização dos expoentes na resolução, será empregado um fonte maior.
Tratando separadamente as expressões, temos que:
\sqrt [4]{8} = 8^{\frac{1}{4}} = (2^3)^{\frac{1}{4}} = 2^{\frac{3}{4}}\\
\enspace \\
\sqrt [5]{16} = 16^{\frac{1}{5}} = (2^4)^{\frac{1}{5}} = 2^{\frac{4}{5}} \\
\enspace \\
\sqrt [20]{8^{13}} = 8^{\frac{13}{20}} = (2^3)^{\frac{13}{20}} = 2^{\frac{39}{20}} \\Então, fazendo as substituições na expressão original, temos:
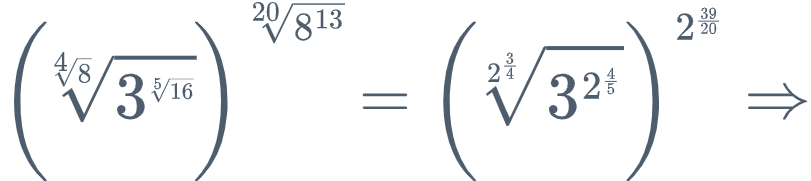
Empregando as propriedades de expoentes, temos: