Address
304 North Cardinal St.
Dorchester Center, MA 02124
Work Hours
Monday to Friday: 7AM - 7PM
Weekend: 10AM - 5PM
Address
304 North Cardinal St.
Dorchester Center, MA 02124
Work Hours
Monday to Friday: 7AM - 7PM
Weekend: 10AM - 5PM

Um carro em movimento uniformemente variado percorre um trecho retilíneo de uma estrada, e o diagrama horário de sua velocidade escalar está esboçado na figura.
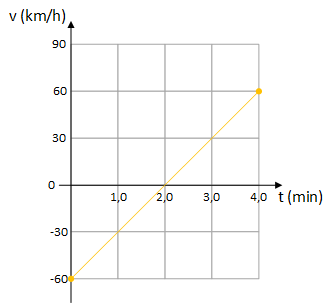
Determine:
Trata-se de uma questão que pode ser resolvida integralmente a partir do gráfico, quase que sem contas. O enunciado diz que o há um carro em MUV (na verdade, nem precisava dizer isso, pois um gráfico de velocidade, representando por uma função de primeiro grau, com inclinação maior que 0 \degree e menor que 90 \degree é sempre MUV).
O gráfico apresenta escala e unidades (km/h e min) e servirá como base para todo o processo de solução.
A velocidade escalar iniciar é aquela indicada pelo gráfico no instante t = 0 \enspace min , como indicado a seguir:
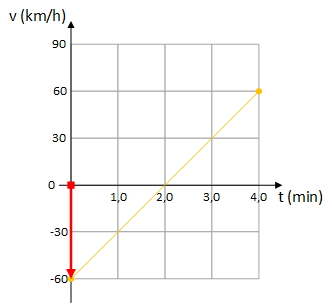
Portanto, a velocidade escalar inicial é -60 \enspace km/h .
Quando temos o gráfico da velocidade em função do tempo, para calcularmos o deslocamento num intervalo de tempo, basta calcularmos a área do gráfico no intervalo em questão. O problema pede para o intervalo [2,0 min ; 4,0 min ] , assim precisamos calcular a área hachurada indicada na figura a seguir:
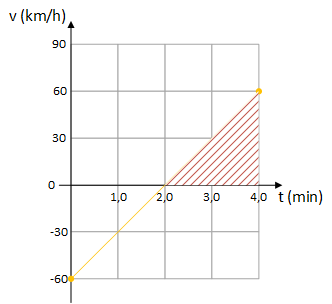
Trata-se da área de um triângulo, então o deslocamento é:
D = \frac{(4 - 2) min \cdot 60 km/h}{2} = \frac{2 min \cdot 60 km / 60 min}{2} = 1kmSemelhante ao item anterior, mas para o intervalo [1,0 min ; 3,0 min ] . Aqui vale reforçar que a questão pede o deslocamento escalar, assim devemos subtrair da área acima do eixo x a área abaixo do mesmo eixo. Nesse caso, estamos calculando o deslocamento em relação ao referencial estabelecido no problema.
Observe que, se fosse pedido o deslocamento absoluto, as áreas seriam somadas e estaríamos calculando quanto o carro se deslocou em relação a um outro referencial, com origem no início do movimento do carro.
Para resolver o item precisamos subtrair da área vermelha a área azul, como indicado na figura a seguir:
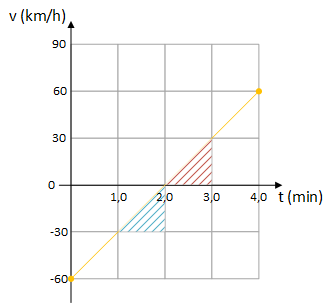
A parttir da figura, verificamos que as áreas são iguais e que o deslocamento escalar no intervalo em questão é 0 km .
O movimento tem uma inversão de sentido no ponto onde a velocidade muda de sinal, isto é, no ponto onde o gráfivo de v cruza o eixo x , como indicado na fugura a seguir:
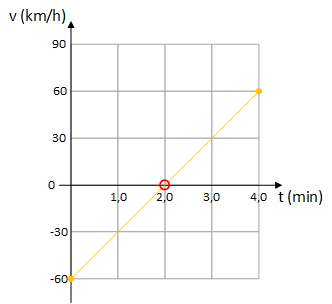
O instante da inversão de sentido é t = 2 min .