Address
304 North Cardinal St.
Dorchester Center, MA 02124
Work Hours
Monday to Friday: 7AM - 7PM
Weekend: 10AM - 5PM
Address
304 North Cardinal St.
Dorchester Center, MA 02124
Work Hours
Monday to Friday: 7AM - 7PM
Weekend: 10AM - 5PM
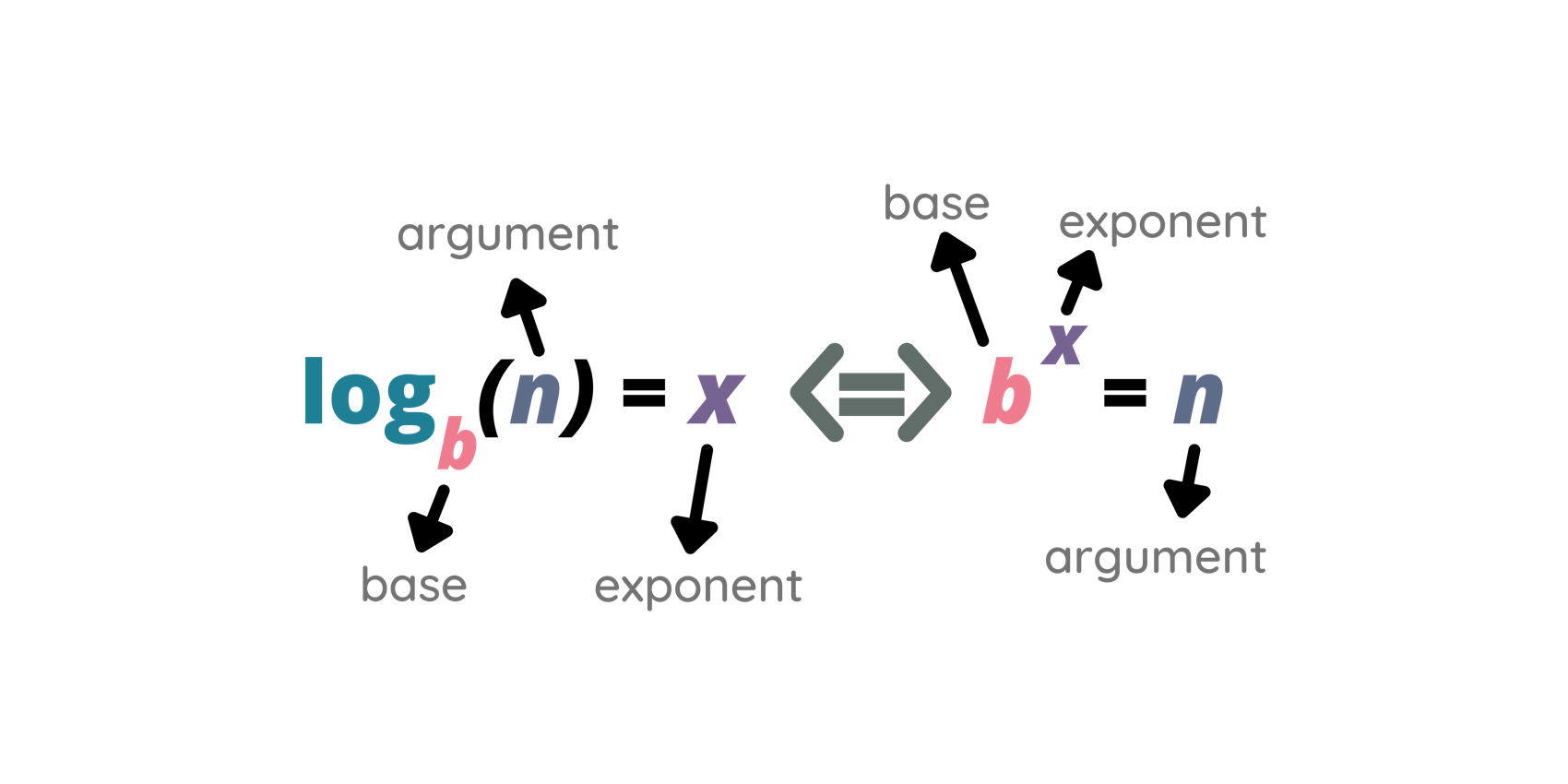
Determine o valor de A tal que 4^{\log_2 A} + 2A - 2 = 0 .
Uma equação logarítmica que usa também exponenciais. é o tipo de exercício que exige um pouco mais de maturidade e iniciativa para a sua resolução. Os cálculos chegam a ser complexos, mas o aluno precisa encontrar uma forma de simplificar a expressão e isso exige mais iniciativa.
Neste caso, em particular, vamos fazer uma substituição de variável que vai simplificar bastante o processo de solução.
Supondo que \log_2 A = m e substituindo na equação original, obtemos:
\log_2 A = m \Rightarrow A = 2^m\\
\enspace \\
\text{Substituindo na equação original:} \\
4^{\log_2 A} + 2A - 2 = 0 \\
4^m + 2 \cdot 2^m - 2 = 0 \\
2^{2m}+ 2 \cdot 2^m - 2 = 0 \\
(2^m)^2+ 2 \cdot 2^m - 2 = 0 \\
\enspace \\
\Delta = (2)^2 - 4 \cdot 2 \cdot (-2) = 12 \\
\enspace \\
2^{m} = \frac{-2 \pm \sqrt{12}}{2 \cdot 1} = \frac{-2 \pm 2\sqrt{3}}{2} = -1 \pm \sqrt{3}A solução 2^{m} = -1 - \sqrt{3} , não convém pois -1 - \sqrt{3} \lt 0 . Resta apenas a solução 2^{m} = -1 + \sqrt{3} , então:
2^{m} = -1 + \sqrt{3} \\
\enspace \\
\text{Mas sabemos que } A = 2^m \text{, então:} \\
2^{m} = A = -1 + \sqrt{3} \\