Address
304 North Cardinal St.
Dorchester Center, MA 02124
Work Hours
Monday to Friday: 7AM - 7PM
Weekend: 10AM - 5PM
Address
304 North Cardinal St.
Dorchester Center, MA 02124
Work Hours
Monday to Friday: 7AM - 7PM
Weekend: 10AM - 5PM
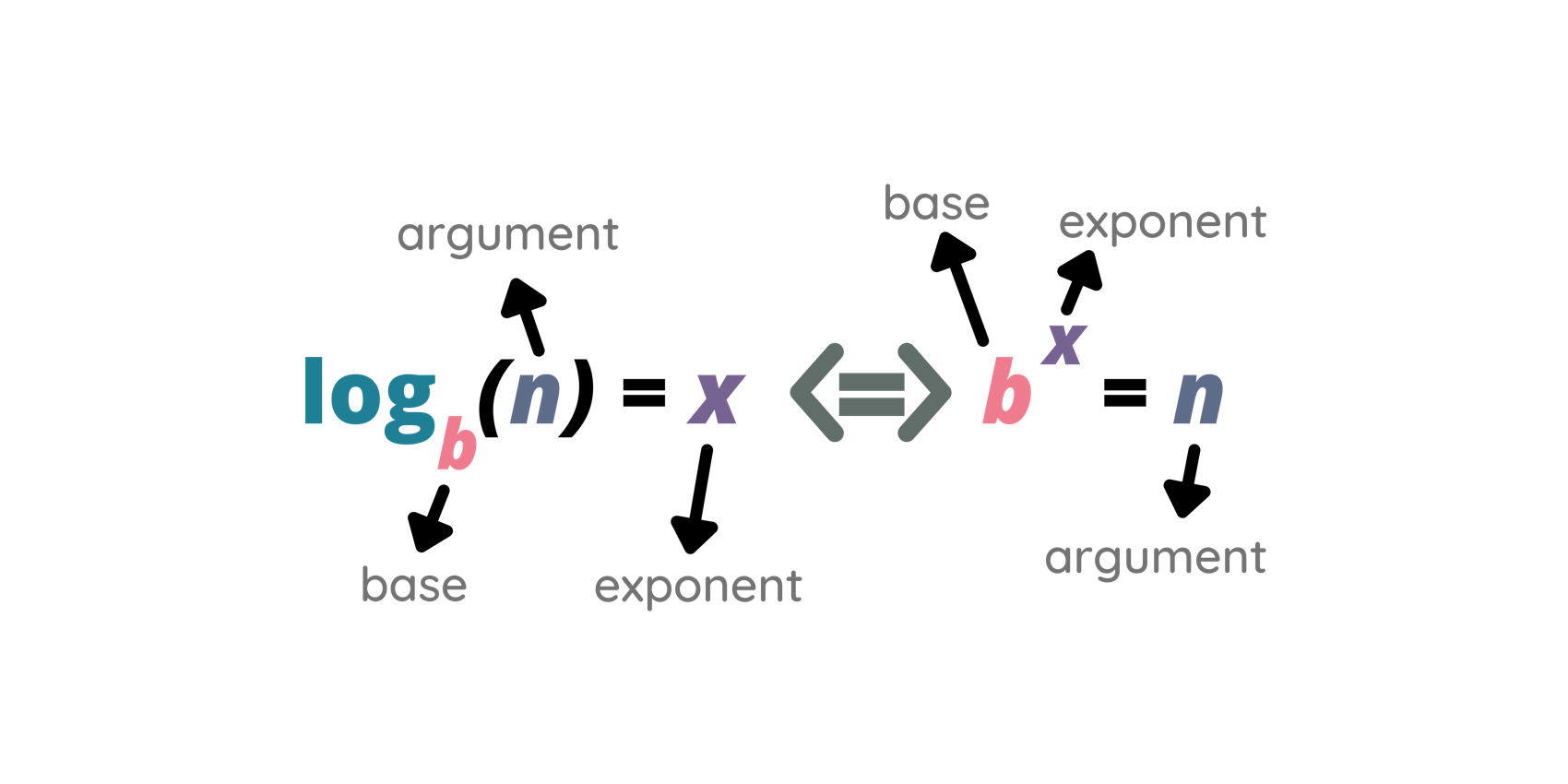
Se a, b, c e d são reais positivos, diferentes de 1 e dois a dois distintos, prove a equivalência:
\dfrac{\log_a d}{\log_c d} = \dfrac{\log_a d - \log_b d}{\log_b d - \log_c d} \Leftrightarrow b^2 = ac .
Para demonstrar a identidade pedida no exercício, é preciso trabalhar algebricamente a expressão, utilizando-se das propriedades dos logaritmos, como qualquer outra questão que apresenta uma equação logarítmica. O diferencial desta questão está em que ela demanda um bocado de iniciativa por parte do aluno e bastante atenção nos cálculos.
Partindo da igualdade à esquerda da expressão original do problema, temos:
\dfrac{\log_a d}{\log_c d} = \dfrac{\log_a d - \log_b d}{\log_b d - \log_c d} \Rightarrow
\dfrac{\dfrac{\log_d d}{\log_d a}}{\dfrac{\log_d d}{\log_d c}} = \dfrac{\dfrac{\log_d d}{\log_d a} - \dfrac{\log_d d}{\log_d b}}{\dfrac{\log_d d}{\log_d b} - \dfrac{\log_d d}{\log_d c}} \\ \enspace \\
\dfrac{\dfrac{1}{\log_d a}}{\dfrac{1}{\log_d c}} = \dfrac{\dfrac{1}{\log_d a} - \dfrac{1}{\log_d b}}{\dfrac{1}{\log_d b} - \dfrac{1}{\log_d c}} \Rightarrow \dfrac{\log_d c}{\log_d a} = \dfrac{\dfrac{\log_d b - \log_d a}{\log_d a \cdot \log_d b}}{\dfrac{\log_d c - \log_d b}{\log_d b \cdot \log_d c}} \\
\enspace \\
\dfrac{\log_d c}{\log_d a} = \dfrac{\dfrac{\log_d {b/a}}{\log_d a \cdot \log_d b}}{\dfrac{\log_d {c/b}}{\log_d b \cdot \log_d c}} \Rightarrow \dfrac{\log_d c}{\log_d a} = \dfrac{\dfrac{\log_d {b/a}}{\log_d a \cdot \log_d b}}{\dfrac{\log_d {c/b}}{\log_d b \cdot \log_d c}} \\
\enspace \\
\dfrac{\log_d c}{\log_d a} = \dfrac{\log_d {b/a} \cdot \log_d b \cdot \log_d c}{\log_d a \cdot \log_d b \cdot \log_d {c/b}} \Rightarrow 1 = \dfrac{\log_d {b/a}}{\log_d {c/b}} \\
\enspace \\
\log_d {c/b} = \log_d {b/a} \Rightarrow \dfrac{c}{b} = \dfrac{b}{a} \\
\enspace \\
\therefore b^2 = acObservação importante, a exigência de a, b, c e d serem reais positivos, diferentes de 1 é o que possibilita a, b, c e d serem usados como logaritmandos e bases ao longo das resolução anterior. Já a, b, c e d serem dois a dois distintos permite com que não haja denominador nulo nas frações.