Address
304 North Cardinal St.
Dorchester Center, MA 02124
Work Hours
Monday to Friday: 7AM - 7PM
Weekend: 10AM - 5PM
Address
304 North Cardinal St.
Dorchester Center, MA 02124
Work Hours
Monday to Friday: 7AM - 7PM
Weekend: 10AM - 5PM
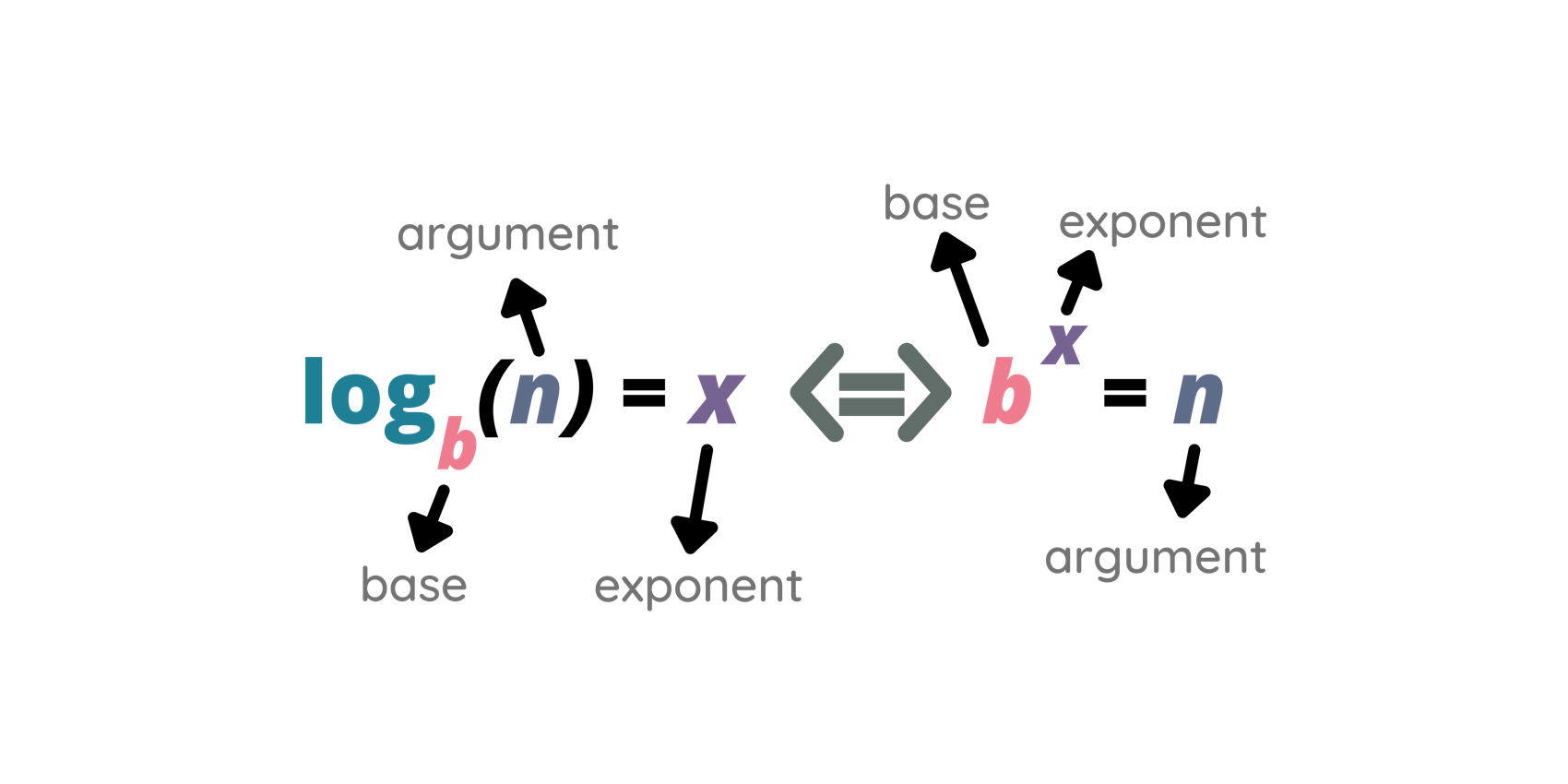
Se 0 < x \ne 1 , demonstre que:
\frac{1}{\log_x 2 \cdot \log_x 4} + \frac{1}{\log_x 4 \cdot \log_x 8} + ... + \frac{1}{\log_x 2^{n-1} \cdot \log_x 2^n} = \left( 1 - \frac{1}{n} \right) \cdot \frac{1}{\log^2_x 2}Sugestão: \dfrac{1}{n(n-1)} = \dfrac{1}{n-1} - \dfrac{1}{n} .
Esta é a típica questão que assusta o aluno: ela exige bastante maturidade e iniciativa, além de apresentar uma soma infinita, o que costuma nos dar alguma inquietude.
Mas, como em toda questão de logaritmos, devemos ficar atentos para a aplicação das propriedades, elas são sempre úteis. E temos que olhar para a expressão da questão com bastante “desconfiança”, procurando encontrar a melhor propriedade a ser usada, no sentido de simplificar expressão original.
O examinador deu ainda uma sugestão, colocando uma igualdade. Na prática, é uma ordem, não uma sugestão! Temos que buscar uma forma de usar a igualdade sugerida, pois ela vai, com certeza, no ajudar na solução da questão.
Além disso, assim como num produto infinito temos que encontrar uma forma de chegar num corta-corta de numeradores e denominadores, numa soma infinita, quase sempre a solução passa por chegar num cancelamento de fatores positivos e negativos que simplificará a solução.
Vamos então em busca de: aplicar propriedades de logaritmos; usar a igualdade sugerida pelo examinador bonzinho; e cancelar fatores positivos e negativos na soma infinita.
Aplicando as propriedades dos logaritmos à expressão original, temos:
\frac{1}{\log_x 2 \cdot \log_x 4} + \frac{1}{\log_x 4 \cdot \log_x 8} + ... + \frac{1}{\log_x 2^{n-1} \cdot \log_x 2^n} = \\
\enspace \\
= \frac{1}{\log_x 2 \cdot \log_x 2^2} + \frac{1}{\log_x 2^2 \cdot \log_x 2^3} + ... + \frac{1}{\log_x 2^{n-1} \cdot \log_x 2^n} = \\
\enspace \\
= \frac{1}{\log_x 2 \cdot 2 \log_x 2} + \frac{1}{2 \log_x 2 \cdot 3 \log_x 2} + ... + \frac{1}{(n-1) \log_x 2 \cdot n \log_x 2} = \\
\enspace \\
= \frac{1}{1 \cdot 2 \cdot \log^2_x 2} + \frac{1}{2 \cdot 3 \cdot \log^2_x 2} + ... + \frac{1}{(n-1) \cdot n \cdot \log^2_x 2} = \\
\enspace \\
= \left(\frac{1}{1 \cdot 2} + \frac{1}{2 \cdot 3} + ... + \frac{1}{(n-1) \cdot n} \right) \cdot \frac{1}{\log^2_x 2} \\Observando a expressão:
\frac{1}{1 \cdot 2} + \frac{1}{2 \cdot 3} + ... + \frac{1}{(n-1) \cdot n}Podemos notar que cada um de seus fatores pode ser substituído pela igualdade sugerida pelo examinador: \dfrac{1}{n(n-1)} = \dfrac{1}{n-1} - \dfrac{1}{n} . Assim, temos, na expressão que obtivemos anteriormente:
= \left(\frac{1}{1 \cdot 2} + \frac{1}{2 \cdot 3} + ... + \frac{1}{(n-1) \cdot n} \right) \cdot \frac{1}{\log^2_x 2} = \\
\enspace \\
= \left( \left( \frac{1}{1} - \frac{1}{2} \right) + \left ( \frac{1}{2} - \frac{1}{3} \right)+ ... + \left( \frac{1}{n-1} - \frac{1}{n} \right) \right) \cdot \frac{1}{\log^2_x 2} = \\
\enspace \\
= \left( \frac{1}{1} - \frac{1}{n} \right) \cdot \frac{1}{\log^2_x 2} = \left( 1 - \frac{1}{n} \right) \cdot \frac{1}{\log^2_x 2}