Address
304 North Cardinal St.
Dorchester Center, MA 02124
Work Hours
Monday to Friday: 7AM - 7PM
Weekend: 10AM - 5PM
Address
304 North Cardinal St.
Dorchester Center, MA 02124
Work Hours
Monday to Friday: 7AM - 7PM
Weekend: 10AM - 5PM
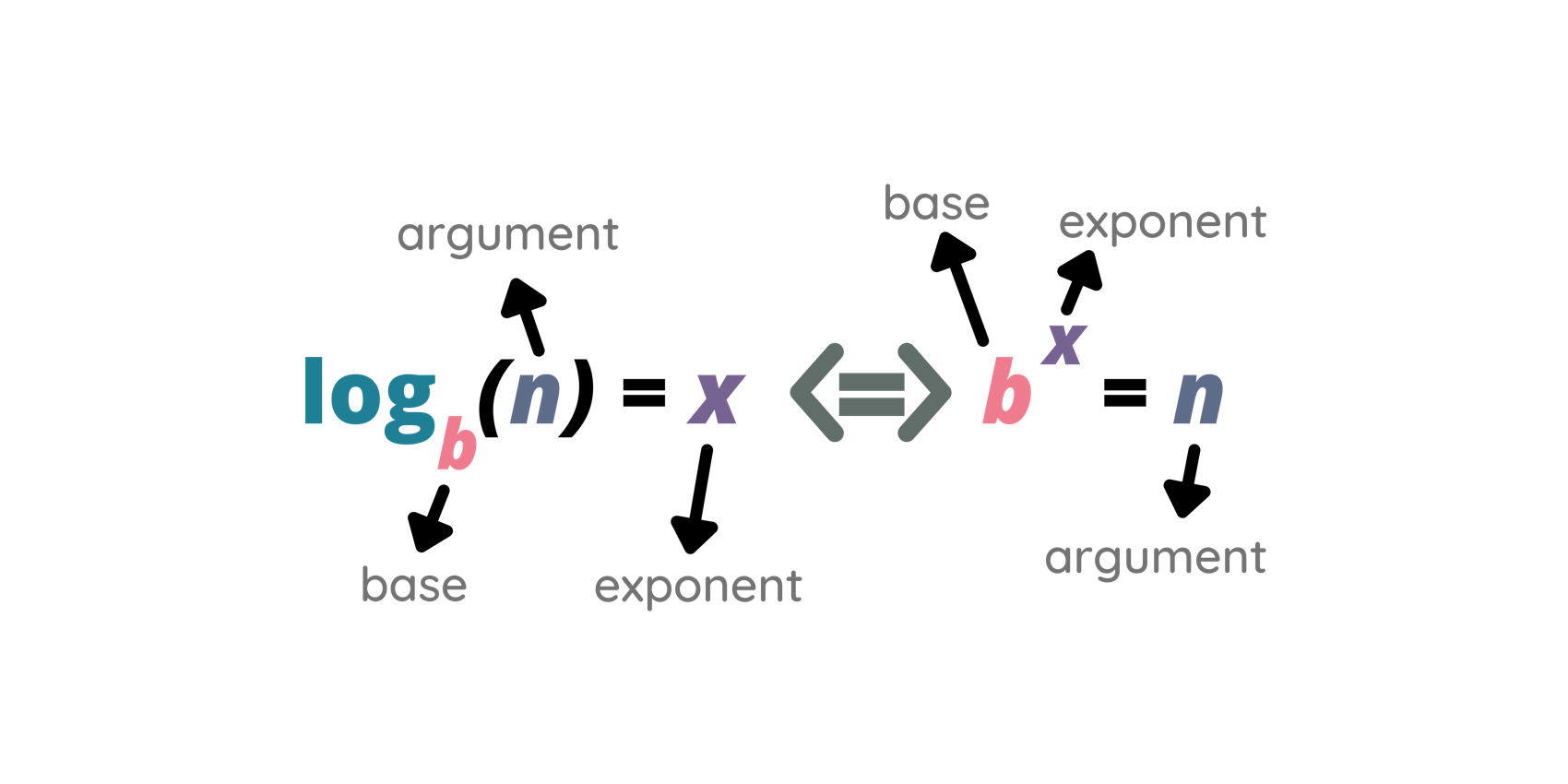
O logaritmo de um número na base 16 é \dfrac{2}{3} . Calcule o logaritmo desse número na base \dfrac{1}{4} .
Exercício de aplicação direta da definição de logaritmos.
Chamando o número desconhecido de x , temos que:
\log_{16} x = \dfrac{2}{3} \Rightarrow x = 16^{\frac{2}{3}} \\
\enspace \\
\text{Calculando o logaritmo desse número na base } \dfrac{1}{4} \text{, temos:} \\
\enspace \\
\log_{\frac{1}{4}} 16^{\frac{2}{3}} \Rightarrow \frac{2}{3} \cdot \log_{\frac{1}{4}} 16 \\
\enspace \\
\text{Fazendo } \log_{\frac{1}{4}} 16 = y \text{, temos:} \\
\enspace \\
16 = \left( \frac{1}{4} \right)^y \Rightarrow 4^2 = (4^{-1})^y \Rightarrow 4^2 = 4^{-y} \Rightarrow y = -2 \\
\enspace \\
\text{Portanto:} \\
\enspace \\
\log_{\frac{1}{4}} x = \frac{2}{3} \cdot \log_{\frac{1}{4}} 16 = \frac{2}{3} \cdot (-2) = - \frac{4}{3}