FME02 – Cap 03 – Ex. 196

Enunciado

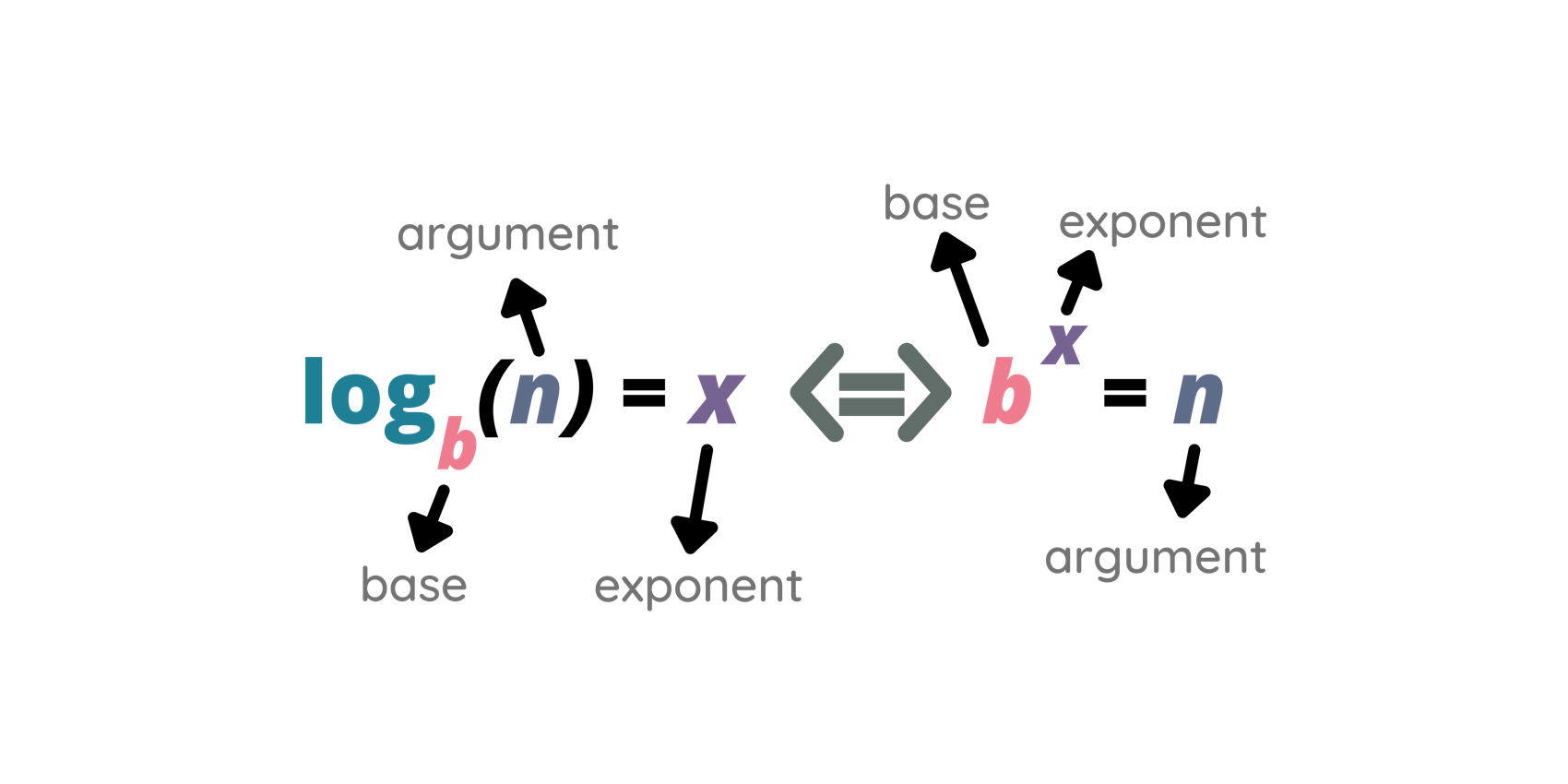
Se a, b, c e d são reais positivos, a [/ katex] e [katex] c diferentes de 1 , prove que:

\log_a b^{(\log_c d)} = \log_c d^{(\log_a b)}

Entendimento

Toda demonstração exige iniciativa, seja para experimentar alternativas de solução, seja para transforma a expressão original, sem saber bem se uma eventual transformação nos levará mais próximo da solução ou não.

Como se trata de uma questão de logaritmos, um bom ponto de partida são as propriedades de logaritmos.

Resolução

Aplicando a propriedade de logaritmo de exponencial na expressão do lado esquerdo da igualdade, temos:

\log_a b^{(\log_c d)} = \log_c d \cdot \log_a b = \log_a b \cdot \log_c d =\log_c d^{(\log_a b)} \\
\enspace \\
\therefore \log_a b^{(\log_c d)} = \log_c d^{(\log_a b)}