Address
304 North Cardinal St.
Dorchester Center, MA 02124
Work Hours
Monday to Friday: 7AM - 7PM
Weekend: 10AM - 5PM
Address
304 North Cardinal St.
Dorchester Center, MA 02124
Work Hours
Monday to Friday: 7AM - 7PM
Weekend: 10AM - 5PM

Um barco está inicialmente parado, encostado em uma das margens de um rio de margens paralelas. A água do rio tem, em relação às margens, velocidade \vec{v}_{AM} cujo módulo é |v_{AM}| = 8,0 \enspace m/s . A partir do instante t = 0 , o barco começa a movimentar-se com movimento retilíneo uniformemente variado em relação à água, cuja aceleração escalar é \alpha = 4,0 \enspace m/s^2 de modo que o eixo do barco fique perpendicular à correnteza.
Um barco encontra-se parado numa das margens de um rio e depois o atravessa, com MUV. O enunciado dá a velocidade das águas e a aceleração do barco.
A situação do problema pode ser esquematizada pela figura a seguir:

É uma questão clássica de composição de movimentos. Esta tem um elemento de diferencial pois o barco se move com o um MUV, mas fora isso, nada de muito diferente para o entendimento da questão.
Um aspecto muito importante é identificar qual o sentido do movimento do barco em relação às margens ou às águas, pois isso permitirá identificar o ângulo formado entre a velocidade vetorial do barco e a velocidade vetorial das águas. No caso do exercício o ângulo é 90 \degree em relação às águas.
Ele pergunta qual a trajetória do barco ao longo da travessia. Bom, instintivamente a gente já pode supor que a trajetória será parabólica, pois se a velocidade vertical do barco vai aumentar (MUV) e a horizontal ficará constante, cada vez mais, a cada intervalo de tempo, o barco vai progredir mais na vertical do que na horizontal, como indicado na figura a seguir:

Podemos pensar este exercício de forma análoga ao arremesso de um objeto a partir do alto de um edifício. Por isso o movimento é de uma parábola.
Mas eu achei pergunta meio inesperada e um pouco mal feita pois, no meu entendimento, o enunciado deveria ter pedido a equação da trajetória, enfim…
É um problema de composição de movimentos e vamos levar em conta, separadamente, o movimento vertical e o horizontal do barco.
Horizontalmente é um movimento uniforme com velocidade constante v_x = 8 \enspace m/s \Rightarrow s_x = s_{0_x} + v_{0_x} \cdot t \Rightarrow s_x = 8 \cdot t .
Verticalmente é um movimento uniformemente variado de equação s_y = s_{0_y} + v_{0_y} \cdot t + \frac{1}{2} \alpha t^2 \Rightarrow s_y = 2 \cdot t^2.
Trabalhando as duas equações anteriores, temos:
s_x = 8 \cdot t \Rightarrow t = \frac{s_x}{8} \\
\text{Substituindo em } s_y \text{ temos:} \\
s_y = 2 \cdot \left( \frac{s_x}{8} \right)^2 \Rightarrow s_y = \frac{{s_x}^2}{32}
Bastante simples, basta considerar que a velocidade vertical v_y é resultante de um MUV, cuja equação é:
v_y = 4 \cdot t
Além disso, sabemos que a velocidade horizontal v_x das águas do rio é constante e tal que v_x = 8.
Assim a velocidade do barco no instante t = 1,0 s é a resultante v_x e v_y . Como o ângulo entre v_x e v_y é 90 \degree , o módulo da velocidade resultante \vec{r} é dado pela hipotenusa do triângulo destacado na figura a seguir:
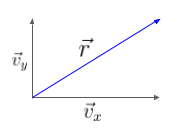
Também achei que a pergunta não está muito bem feita pois o enunciado diz “velocidade”, mas o que ele quer mesmo é a velocidade escalar ou o módulo da velocidade vetorial naquele instante, mas enfim…
Portanto, temos que:
v_x = 8 \\
v_y = 4 \cdot 1 \\
\enspace \\
r^2 = {v_x}^2 + {v_y}^2 \\
r^2 = 8^2 + 4^2 \Rightarrow r = \sqrt{80} \\
\Rightarrow r = 4\sqrt{5}