FC01 – Cap 06 – Ex. 14

Enunciado

Do alto da Torre de Pisa, Galileu abandonou da sacada de altura H uma bala de canhão B_1 , a qual despencou em queda livre até o solo. Nesse mesmo instante, o seu aluno Adamo também abandonou, de uma segunda sacada da torre, de altura h , uma outra bala de canhão B_2 , a qual também despencou em queda livre. Entre a queda da bala B_1 e a queda da bala B_2 foi constatada uma diferença de tempo de 0,60 s .

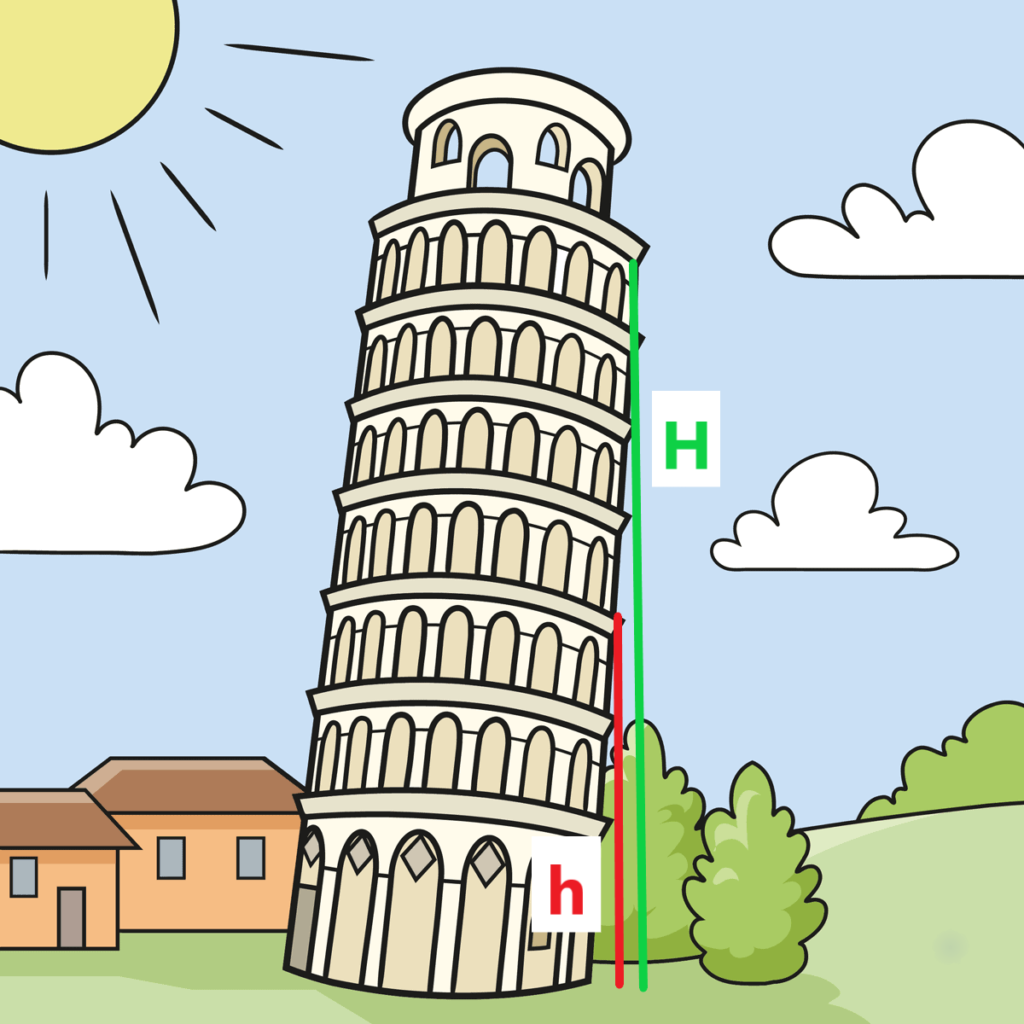
Sabendo que h = 0,64H e g = 10 \enspace m/s^2 , podemos afirmar que os tempos de queda das balas B_1 e B_2 são, respectivamente:

1. 3,0 s \text{ e } 2,4s
2. 3,0 s \text{ e } 0,6s
3. 2,4 s \text{ e } 2,0s
4. 2,4 s \text{ e } 3,0s
5. 2,4 s \text{ e } 2,8s

Entendimento

Bom, aqui temos uma referência ao clássico experimento do Galileu na Torre de Pisa. Entendendo fisicamente o problema, temos: duas balas B_1 e B_2 são abandonadas (isto é, ambas partem de v_0 = 0 \enspace m/s ) de alturas diferentes na torre, ao mesmo instante.

O problema dá a aceleração da gravidade, a diferença em segundos entre a queda de uma bala e da outra, bem como a diferença proporcional entre as alturas de queda ( h = 64\% \text{ de }H ).

Para resolver este problema, basta usarmos as equações do MUV (queda livre é apenas um caso especial de MUV) e levarmos em conta a diferença entre os tempos de queda das duas balas.

Resolução

Considerando t_{B_1} como o tempo de queda e v_{B_1} como a velocidade final da bala B_1 , temos, aplicando Torricelli:

v_{B_1}^2 = v_{0_{B_1}}^2 + 2a \Delta s_{B_1} \\
v_{B_1}^2 = 0^2 + 2 \cdot 10  H \\
v_{B_1} = \sqrt{20H} = 2 \sqrt{5H}

Considerando t_{B_2} como o tempo de queda e v_{B_2} como a velocidade final da bala B_2 , temos, aplicando Torricelli:

v_{B_2}^2 = v_{0_{B_2}}^2 + 2a \Delta s_{B_2}\\
v_{B_2}^2 = 0^2 + 2 \cdot 10  h \\
v_{B_2} = \sqrt{20h} = 2 \sqrt{5h} = 2 \sqrt{5 \cdot 0,64H} = 1,6 \sqrt{5H}

Aplicando a equação da velocidade no MUV para as duas balas, temos:

v_{B_1} = v_{0_{B_1}} + a \cdot t_{B_1} \\
v_{B_1} = 0+ 10 \cdot t_{B_1} \\
v_{B_1} = 10 \cdot t_{B_1} \Rightarrow 2 \sqrt{5H} = 10 \cdot t_{B_1} \\
\enspace \\
v_{B_2} = v_{0_{B_2}} + a \cdot t_{B_2} \\
v_{B_2} = 0+ 10 \cdot t_{B_2} \\
v_{B_2} = 10 \cdot t_{B_2} \Rightarrow 1,6 \sqrt{5H} = 10 \cdot t_{B_2} \\
\enspace \\
\text {Mas como } B_2 \text{ cai de uma altura mais baixa, temos:} \\
t_{B_2} = t_{B_1} - 0,60 \\
\enspace \\
\text {Assim:} \\
2 \sqrt{5H} = 10 \cdot t_{B_1} \\
1,6 \sqrt{5H} = 10 \cdot (t_{B_1} - 0,60)

Subtraindo uma equação da outra, obtemos:

2 \sqrt{5H} - 1,6 \sqrt{5H} = 10 \cdot t_{B_1} - 10 \cdot (t_{B_1} - 0,60) \\
0,4 \sqrt{5H} = 0,60 \Rightarrow \sqrt{5H} = \frac{6}{0,4} \\
5H = 15^2 \Rightarrow H = 45m

Substituindo o valor H em 2 \sqrt{5H} = 10 \cdot t_{B_1} , temos: 2 \sqrt{5 \cdot 45} = 10 \cdot t_{B_1} \Rightarrow 2 \cdot 15 = 10 \cdot t_{B_1} \Rightarrow t_{B_1} = 3,0s

Como t_{B_2} = t_{B_1} - 0,60 , temos que t_{B_2} = 2,4s .

A resposta é alternativa A.

Resolução Alternativa

Como estratégia de solução alternativa há uma bastante não convencional, mas que, apesar de não usar quase nenhum conceito de Física, pode economizar tempo de prova.

Observando as alternativas, três delas não têm a diferença entre os tempos de 0,6s e estão descartadas, restando alternativas A e D como viáveis.

Analisando as alternativas de A e D, podemos notar que apenas a alternativa A tem tempo de queda para bala B_2 menor o tempo de queda da bala B_1 , o que atende as condições do problema.

Dessa forma, a única alternativa viável é a alternativa A, que é a correta.

Em geral, nas provas de vestibular, as alternativas são mais bem construídas do que as dessa questão. Assim, não é sensato esperar esse tipo de moleza num vestibular de verdade.